https://arxiv.org/abs/2002.08709
Introduction
DNNは非常に高い表現力を持つため、簡単に過学習をしてしまう。train loss, test lossが同時に下がる状況では理想的だが、さらに学習すると以下のように過学習する=train lossは下がるがtest lossは上がっていく。
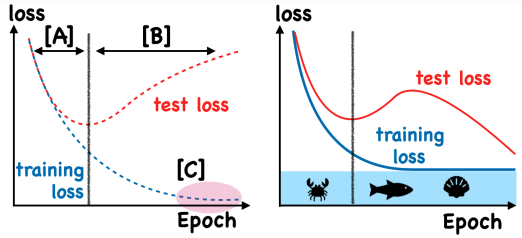
提案する新しい手法は、ある閾値を設けてそれを下回るならgradient ascendすることで、過学習を防げるという提案。
底部に水を入れて浮かばせるといういみでfloodingらしい。
これは数式では、当初のObjectiveがだとすると、以下のように修正をすればいい。
outputs = model(inputs)
loss = criterion(outputs, labels)
flood_loss = (loss - b).abs() + b
optimizer.zero_grad()
flood_loss.backward()
optimizer.step()元々以上の場合は恒等であり、下回った場合はを最低値として、最大でまで増えていく。
という閾値の前後を動いたりするが、これはランダムウォークにあたり、よりよい平坦な領域へ行くことが予想されている。
既存の正則化手法は、パラメタのノルムを小さく制限する、DNNの活性度を下げる、soft labelにする、early stoppingであるが、真新しいものを導入した。併用可能である。
また、既存の手法で正則化をしてもover parametroizedなDNNでは訓練損失が0に行くのは不可避である。
Background
正則化手法
L2ノルムを制約する、ドロップアウトするなどの手法で過学習を防ぐものがある。
重み減衰、ドロップアウト、early stoppingなどがL2ノルム正則化と同じ効果を持つとわかっている。L1ノルムで正則化するものもある。
Data Augmentationというそもそもデータを偽のように増やして、学習させるのおある、
Over Parameterizeした際の二重降下曲線

Belkin, M., Hsu, D., Ma, S., and Mandal, S. Reconciling modern machine-learning practice and the classical bias–variance trade-off. PNAS, 116:15850–15854, 2019.
上の論文で提唱されてるように、パラメタを増やしていくとある値を境に、急激にtest riskも小さくなる。つまり、より大きなモデルほど高い汎化性能を獲得する。
これは線形回帰でも同じ現象がみられているうえ、どうやらエポック数の関数としてもこれを見ることができるとのこと。
Nakkiran, P., Kaplun, G., Bansal, Y., Yang, T., Barak, B., and Sutskever, I. Deep double descent: Where bigger models and more data hurt. In ICLR, 2020.
Weakly supervised Learningにおける経験的リスクの最小化の回避
弱教師あり学習では、特に経験リスクが負になることが重大な問題を呼ぶらしい。これと似た動機を考えている。
Early Stoppingは負になる問題の解決策になりえるが、あまりにアルゴリズム別に依存していて不安定である。
各種の先行研究との比較
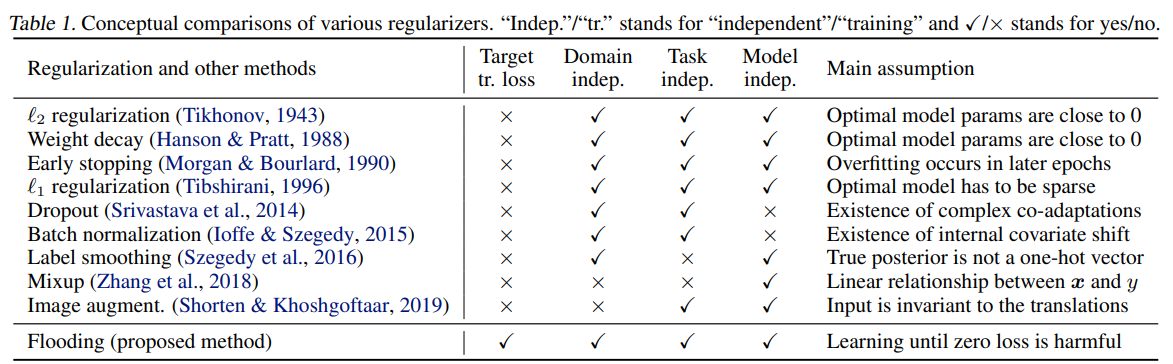
横軸の項目は「training lossを目的とするか」、「個別ドメイン非依存しているか」、「個別タスク非依存か」、「個別モデル非依存か」
提案手法
前提条件
- がデータで、ラベルは。
- 識別器。
- 損失はクロスエントロピー損失を採用。
提案アルゴリズム
先ほども言ったようにする。
outputs = model(inputs)
loss = criterion(outputs, labels)
flood_loss = (loss - b).abs() + b
optimizer.zero_grad()
flood_loss.backward()
optimizer.step()このはまさにハイパラで、うまく探索するしかない。
実装
ミニバッチごとに学習してパラメタを更新するので、個のミニバッチがあるとき、そのように計算したときの損失は、真の損失を上から押さえる。
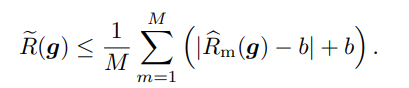
実験
なんとFloodingは一般化性能までよくするらしい。
合成データセット
- ガウス分布からサンプリングした合成データセット。
- sinデータセット。
- スパイラルデータ
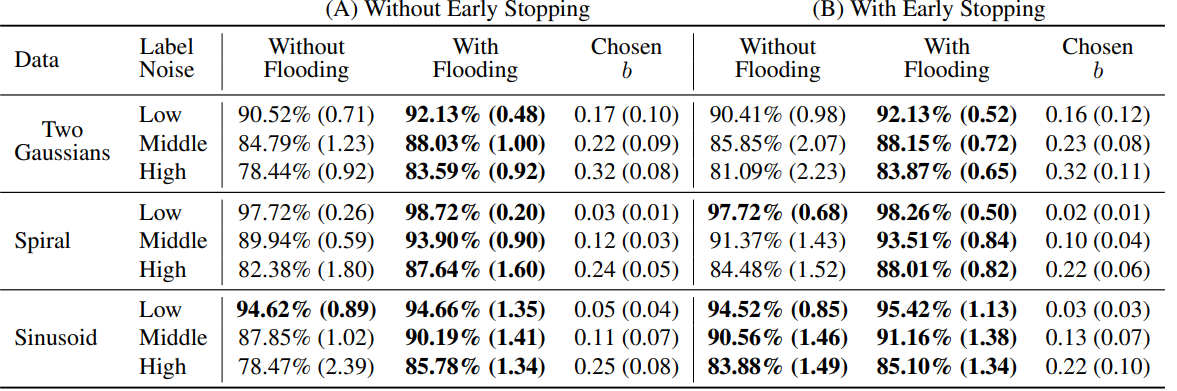
Floodingすると、汎化性能までちゃんとよくなるとわかる。
ベンチマークデータセット
- MNIST
- Kuzushiji-MNIST
- SVHN
- CIFAR10
- CIFAR100
それぞれFloodingで性能向上が見られた。
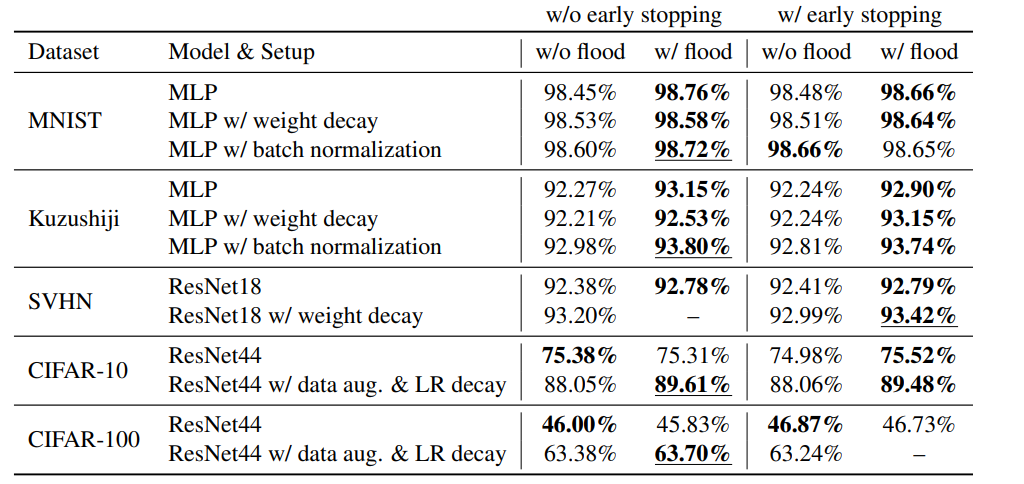
Floodingは汎化性能も向上させるか
- Floodingを加えた後でも、記憶性能を保持できるか?Floodingの閾値を挙げると、以下のようにtraining accuracyが下がる。これを、汎化性能が上がっていると主張している。
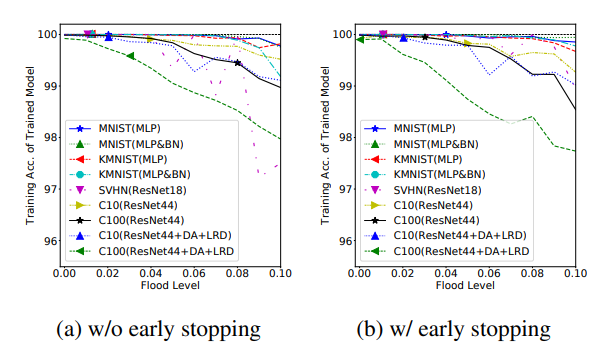
- Floodingを加えると、勾配が一定以上のサイズを保ちやすく、その結果局所最適解に陥りづらくなる。
Floodingがうまくいく理由の示唆
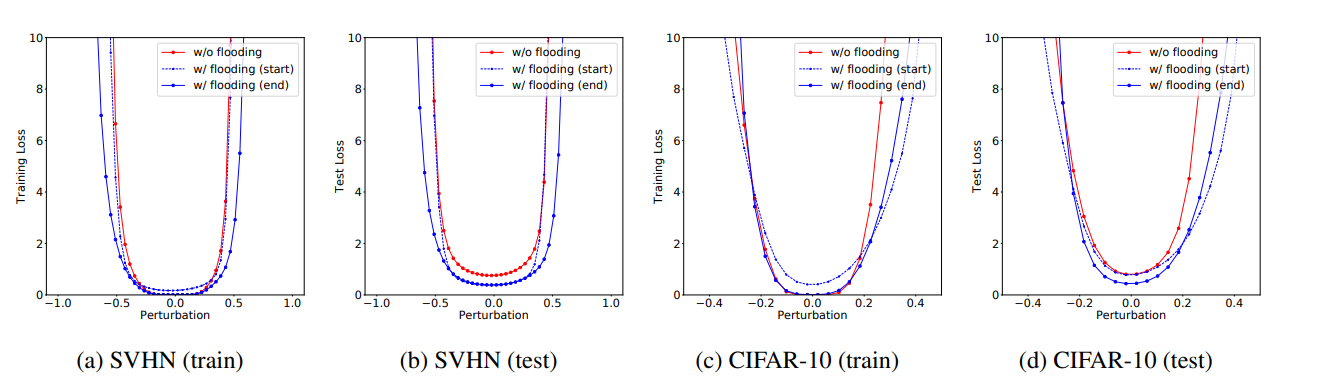
特にtestにおいて、最適解の近くである程度ランダムで動かしても、赤線よりも青い線のほうが平たんだとわかる。
青実線がFloodingで何回も周りをランダムウォークした時の点。青い点線はFloodingではじめて絶対値の中が負になった点。何回も周りをランダムウォークしたら、よくなっていると期待できる。
